什么是圆环展开

顾名思义，将指定圆环展开为矩形。

几何基础

如下图所示，圆环内径为r，外径为R，圆心为O。

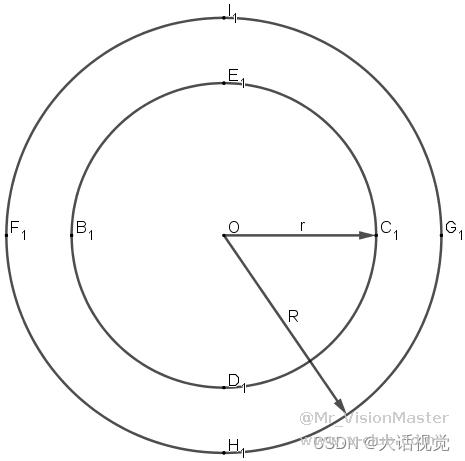
设圆心O坐标为(x0,y0)，射线PO到射线OC1的夹角为θ，由几何知识可知：
内圆上点P的坐标(x,y)为：
x = x0 + r * cosθ
y = y0 - r * sinθ
外圆上点P’的坐标(x’,y’)为：
x’ = x0 + R * cosθ
y’ = y0 - R * sinθ
同理可知，若点P落在以O为圆心，半径为Radius(r≤Radius≤R)的圆周上，则其坐标(X,Y)为：
X = x0 + Radius * cosθ
Y = y0 - Radius * sinθ

原理推导

首先要确定展开矩形图像的宽和高。在此，我们不假思索地给出以下结论：
DstWidth = (r + R) * 2π * 0.5
DstHeight = R - r
然后，要确定展开矩形图像中，第i行第j列像素点的灰度值。
假设上图中，点C1到G1连线方向为圆环展开的起始方向，由【原理推导】小节结论可知，展开矩形图像中，第i行第j列像素点对应原图像中的坐标为：
x = x0 + (r + i) * cos(j * 2π / DstWidth)
y = y0 - (r + i) * sin(j * 2π / DstWidth)
显然，展开矩形图像中，第i行第j列像素点对应原图像中的像素坐标不为整数，因此需要采用图像插值算法。最常用的图像插值算法包括最近邻插值和双线性插值，后者插值效果更好，但耗时也相对更长。

最近邻插值
最近邻插值示意图如下图所示。

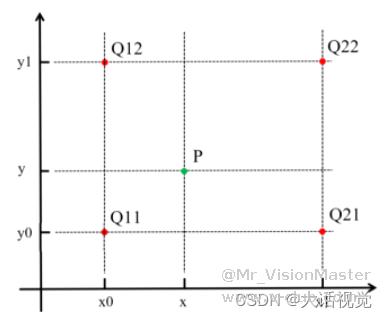
如上图所示，(x0,y0)、(x0,y1)、(x1,y0)、(x1,y1)都是原图像上的坐标点，灰度值分别对应为Q11、Q12、Q21、Q22。而灰度值未知的插值点(x, y)，根据最近邻插值方法的约束，其与坐标点(x0, y0)位置最接近 (即位于(x0,y0)的邻域内)，故插值点(x, y)的灰度值等于Q11。
双线性插值
双线性插值示意图如下图所示。

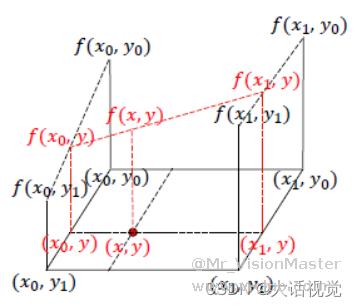
由上图可知，二维图像的双线性插值，需要经过三次一阶线性插值。

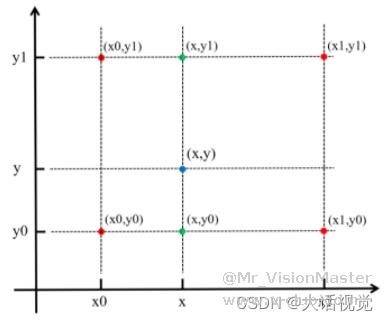
最终插值计算公式为：

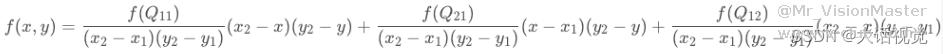
核心代码

// 双线性插值
unsigned char CAlgorithmModule::BilinearInterpolation(float x, float y, MVDSDK_BASE_MODU_INPUT* modu_input, int width, int height)
{
	x = (x < 0) ? 0 : x;
	y = (y < 0) ? 0 : y;
	x = (x > width) ? width : x;
	y = (y > height) ? height : y;

	int x1 = floor(x);
	int x2 = ceil(x);
	int y1 = floor(y);
	int y2 = ceil(y);

	int pos1 = y1 * width + x1;
	int pos2 = y1 * width + x2;
	int pos3 = y2 * width + x1;
	int pos4 = y2 * width + x2;

	unsigned char* pImgData = modu_input->pImageInObj->GetImageData(0)->pData;
	unsigned char grayValue = pImgData[pos1] * (x2 - x) * (y2 - y) + pImgData[pos2] * (x - x1) * (y2 - y) + pImgData[pos3] * (x2 - x) * (y - y1) + pImgData[pos4] * (x - x1) * (y - y1);

	return grayValue;
}

运行结果对比

采集多幅图像，分别采用本文提出的算法、VisionMaster（国内最领先的算法平台，简称VM）进行圆环展开。
VM圆环展开：

本文圆环展开：

可以看出，采用本文方法开发的圆环展开模块运行效果与VM基本一致。
作者衷心希望国产品牌能够扬名世界，而我们每个人亦能为国产产品做出自己的贡献与创新，不断突破国外垄断和技术壁垒。