双目相机标定原理

2761
0
分享

二维码

分享链接
2022-03-24 19:51

RGB-D相机

人类具有一双眼睛，对同一目标可以形成视差，因而能清晰地感知到三维世界。因此，计算机的一双眼睛通常用双目视觉来实现，双目视觉就是通过两个摄像头获得图像信息，计算出视差，从而使计算机能够感知到三维世界。双目标定作为双目相机三维重建的必要环节，目前已经得到广泛研究，使用范围最广的就是张正友标定方法，本文以张氏标定的具体原理为基础，介绍双目标定过程。

一、双目标定简介

双目标定时不仅标定出两个相机的内参，还要标定出两个相机之间的旋转平移关系。标定得到的内参、外参、畸变系数等，是双目视觉进行图片校正、三维重建恢复的基础。

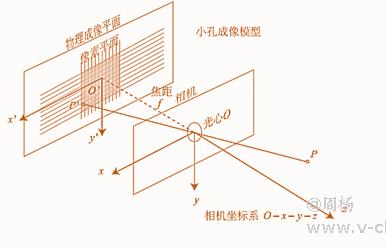
内参：在小孔成像模型中有一个光点P，其将光以直线的方式穿过纸板的小孔(光心），射到显示纸板（物理成像平面）上，其坐标系结构如下图所示。而内参的作用即是在知道P的x、y、z后可以求出x`,y`。

外参：三个轴的旋转参数分别为（ω、δ、 θ）,然后把每个轴的3*3旋转矩阵进行组合（即先矩阵之间相乘），得到集合三个轴旋转信息的R，其大小还是3*3；T的三个轴的平移参数（Tx、Ty、Tz）。R、T组合成成的3*4的矩阵，是转换到标定纸坐标的关键。

畸变参数是：k1,k2,k3径向畸变系数，p1,p2是切向畸变系数。径向畸变发生在相机坐标系转图像物理坐标系的过程中。而切向畸变是发生在相机制作过程，其是由于感光元平面跟透镜不平行。

在进行双目标定时，需要使两个相机对同一标定板进行多次取图，分别标定出各自的内参和相对于标定板的外参，然后便可计算出两相机位置间的关系。

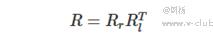
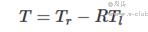
其中，R为两摄像头间的旋转矩阵，T为两摄像头间的平移矩阵。Rr为右摄像头经过张氏标定得到的相对标定物的旋转矩阵，Tr为右摄像头通过张氏标定得到的相对标定物的平移向量。Rl为左摄像头经过张氏标定得到的相对相同标定物的旋转矩阵，Tl为左摄像头经过张氏标定得到的相对相同标定物的平移向量。

通过标定获得的畸变系数，我们可以将图像的畸变消除；通过内参，我们可以变换像素到相机坐标下；通过外参，我们可以变换相机坐标到世界坐标。标定后，双目通过极线校正可以进行光轴的平行，以满足同一目标点在左右图像的同一行上，减少立体匹配的运算量。

二、双目标定原理

这里我们主要介绍张正友标定法。将标定棋盘格放在不同位置和角度进行拍摄，采集的图片数不少于 3 张，一般选用15张左右。

1. 先通过图像处理获得棋盘格的角点，设其像素坐标为[u,v,1]^T，设其世界坐标为X,Y,1，设K为相机内参矩阵，r1_,r2,r3 和t分别为相机坐标系相对于世界坐标系的旋转矩阵和平移向量，棋盘格到图像平面的单应性变换为：

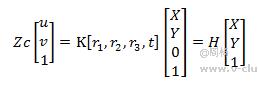
其中设定的相机内参矩阵

，单应性矩阵

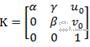
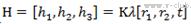
2. 根据旋转矩阵的性质

和

，可以得出内参矩阵K的约束条件，因为内参数矩阵有5个未知数，当采集的标定图片数目≥3 时即可求出内参矩阵K。

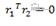
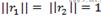
3. 再根据内部参数与映射矩阵求出每幅采集的标定板图像相对于基准图像的旋转矩阵R与平移向量t, 即外参矩阵的参数。对求得的参数根据极大似然原则进行优化，求出极大似然估计值。

4. 将每张图像的控制点根据求解的参数重投影回三维空间，最小化与真实值的差异，建立非线性最小化模型，用LM(Levenberg-Marquardt)迭代算法优化参数。

当然，由于外参矩阵 [r1,r2,t] 和内参矩阵 K 是在有畸变的情况下获得的，这里得到的像素坐标[u,v,1]^T并不是完全理想的、无畸变的。我们的总逻辑是，在进行内参矩阵和外参矩阵的求解的时候，我们假设不存在畸变；在进行畸变系数的求解的时候，我们假设求得的内参矩阵和外参矩阵是无误差的。最后，我们再通过L-M算法对于参数进行迭代优化。