1 标定

当相机平面与物料平面保持水平时，可将世界标系到像素坐标系的映射关系（刚体变换、透视投影、仿射变换）简化为两个二维坐标系之间的仿射变换关系，即物理坐标系与像素坐标系之间的关系，求解关系矩阵的过程称为标定。如果相机与物料之间的高度发生变化时，相机视野会发生变化，此时同一个特征点的像素坐标会发生变化，即像素坐标系发生变化，所以当前高度的标定关系只能用于同样高度的生产场景。
在一个二维坐标系中，一个点相对于原点的旋转、缩放、平移关系矩阵如下所示。那么在两个二维坐标系中，两个坐标系的关系矩阵也存在这样的旋转、缩放、平移关系（仿射变换）。引入第三维方便矩阵运算。

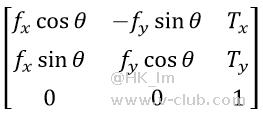
共轴场景中，吸嘴与旋转中心在同一条垂线上，VM推荐9点绝对标定（平移旋转标定模块，平移标定类型），获取9组像素点和物理点，用平移旋转标定模块（同N点标定模块）标定得到绝对标定矩阵；生产时像素点通过此矩阵转换得到机构绝对物理坐标。
不共轴场景中，吸嘴与旋转中心不在同一条垂线上，VM推荐12点相对标定（平移旋转标定模块，平移旋转标定类型），注意区分于9点绝对标定+3点旋转标定（平移标定+旋转标定）。前者获取12组像素点和物理点，此时用平移旋转标定模块标定得到的标定矩阵为相对标定矩阵；生产时像素点通过此矩阵转换得到相对物理坐标，相对物理坐标系原点为拟合的像素旋转中心转物理坐标。
下图左边为9点绝对标定文件，右边为12点相对标定文件，通过观察可以得知两种标定所得到的缩放和旋转关系都是一样，只是平移不同（第三列），即像素点通过标定文件转物理坐标所在的坐标系原点不同。结合12点标定时的第五点像素坐标和绝对物理坐标，“12标定矩阵”也能将像素坐标转绝对物理坐标，具体参考分享《平移旋转标定模块与绝对物理坐标》。

这两个矩阵数据中，无论是9点还是12点标定矩阵，可以发现与上面矩阵略有不同，即下面两个矩阵中不是第二个数与第四个数不同，而是第一个数与第五个数不同。此情况可以用下图两个坐标系进行说明，这两个坐标系中A对应着B，大小比例为1：1，X轴方向相反。

A`点旋转θ角度可以得到B点， A点与A点x坐标相反，则：

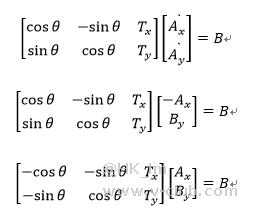
此时矩阵中第一个数与第五个数不同，同样仅当Y轴方向不同时，矩阵中同样是第一个数与第五个数不同，因此说明得到此标定矩阵的两个坐标系存在且仅一个轴的正负方向相反。

2 单相机定位

2.1 单点抓取

共轴场景：机构旋转中心与抓爪共轴，在同一条垂线上。抓爪能够抓取物料时，姿态的俯视效果如下图(a)，绿色位为旋转中心，橙色为物料。当视觉根据图像判断物料的Mark点坐标没有变，物料角度发生45度变换时，机构只需要在基准抓取位旋转45度即可抓取物料。

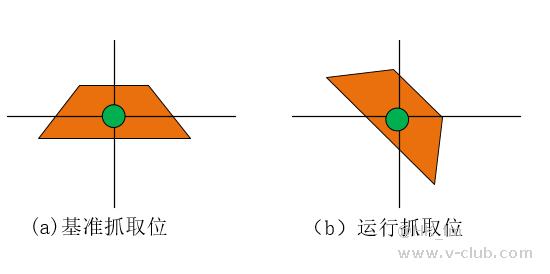
不共轴场景：机构旋转中心与抓爪不共轴，不在同一条垂线上。抓爪能够抓取物料时，姿态的俯视效果如下图(a)，绿色位为旋转中心，橙色为物料。当视觉根据图像判断物料的Mark点坐标没有变，物料角度发生45度变换时，机构旋转45度，抓爪则会产生旋转偏差dx和dy，在这个位置并不能抓起物料，抓爪需要考虑旋转偏差带来的才能真正抓起物料。

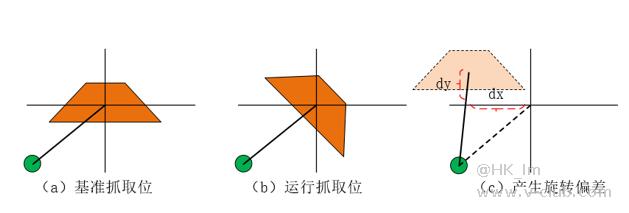
注意，不共轴场景中，当物料为圆形时，即相当于没有角度变化，则仍可以使用9点绝对标定来标定机构绝对物理坐标系和像素坐标系关系，进而只需要计算平移偏差。
针对不同场景，需要选择合适的标定方式。共轴场景9点绝对标定，在生产时只需要计算平移偏差，平移偏差为物理坐标系下运行点减去基准点，示教位加上相对平移偏差进行抓取。不共轴场景12点相对（或9点绝对+3点旋转）标定，在生产时除了计算平移偏差还需要计算旋转偏差。旋转偏差计算分析如下：
（1）不共轴，使用9点绝对+3点旋转标定时，标定的是机构绝对物理坐标系与像素坐标系的关系。9点绝对标定获取绝对标定矩阵M₉，3点旋转标定获取拟合旋转中心Image_center，此时M₉ * Image_center=Physical_center，且物理坐标系中旋转半径R=M₉ * Image_{Mark基准点} - Physical_center。

下图中假设浅红色直线为物料，左边是能够抓取时的姿态，记录示教位坐标T，右边为运行时姿态。对于视觉图像而言，在运行姿态，物料没有发生平移化，只有角度变化，即需要计算旋转偏差。根据运行姿态，抓取时，可以通过示教位绕黑色“旋转中心”旋转计算旋转偏差。

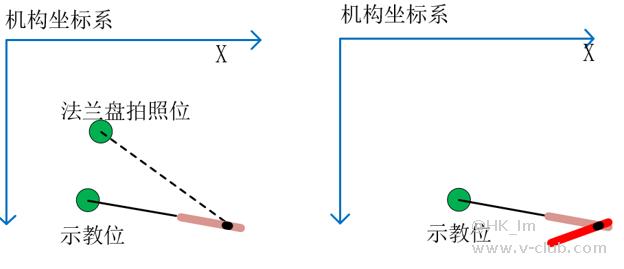
假设相机静止，9点绝对+3点旋转标定时，在第五点机构携带物料旋转（图中黑色点为Mark点），获得旋转半径为R，则机构绝对物理坐标系中黑色“旋转中心”=拍照位（第五点机构位置）+旋转半径（R）。生产时，示教位绕黑色“旋转中心”的旋转可以计算旋转偏差，最后右边运行姿态抓取位置=T+旋转偏差。综合抓取位置=T+旋转偏差+平移偏差。
（2）不共轴，使用VM中12点相对标定时，标定的是机构相对物理坐标系与像素坐标系的关系M₁₂。此时M₁₂ * Image_center= Physical_center =(0,0)^T，即在物理坐标系中，拟合的物理旋转中心为原点。物理坐标系中旋转半径则R=M₁₂ * Image_{Mark基准点} - Physical_center= M₁₂ * Image_{Mark基准点}。获取旋转半径后，当视觉判断物料发生角度变化时，旋转偏差计算如（1）所述。

2.2 单点纠偏

纠偏场景则是机构携带物料运动，通过视觉判断物料的位移变化和角度变化。 同样分为共轴和不共轴标定，其中9点绝对标定，在生产时只需要计算平移偏差，平移偏差为物理坐标系下基准点减去运行点，进而将运行位纠正到基准位；12点相对（或9点绝对+3点旋转）标定，在生产时还需要计算旋转偏差进而计算平移偏差。旋转偏差计算分析如下：
与抓取共同点，物理坐标系中旋转半径R=M₉ * Image_{Mark基准点}-Physical_center，或R=M₁₂ * Image_{Mark基准点} - Physical_center= M₁₂ * Image_{Mark基准点}。与抓取不同点，抓取是机构根据示教位及偏差去到运行位进行抓取；纠偏是机构携带运行位的物料回到基准位，物料一直在机构上。
下图中假设浅红色直线为物料，左边是基准时姿态，中间和右边深红色为运行时姿态。对于视觉图像而言，在运行姿态，物料有角度变化，即需要计算旋转偏差。

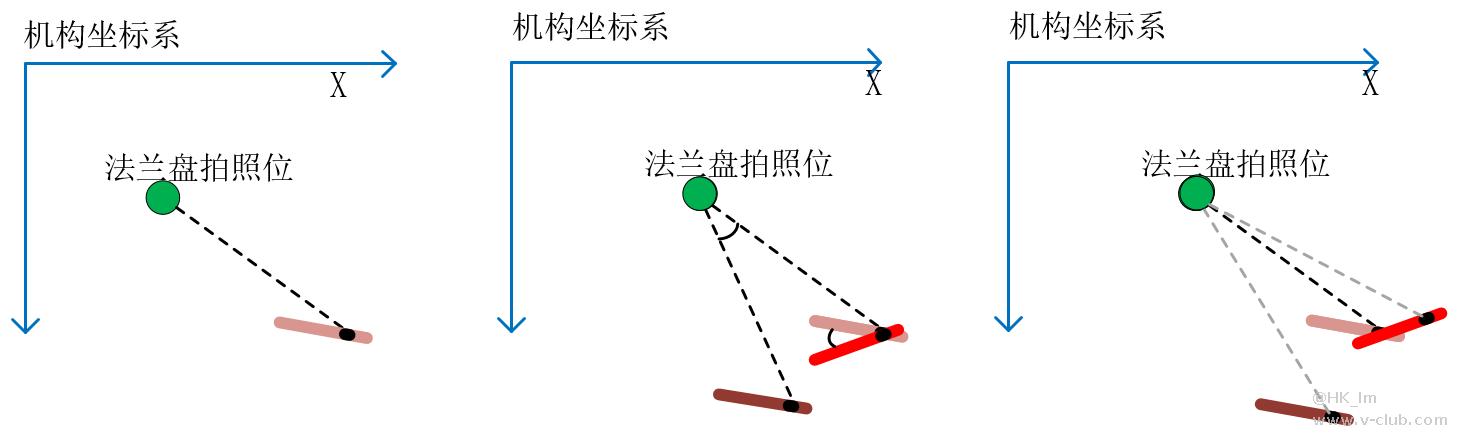
（1）9点绝对+3点旋转标定时，图中黑色点为Mark点，机构绝对物理坐标系中轴长“末端”=M₉ * Image_{Mark运行点} + 旋转半径（R），如右图中的虚线所示。生产时，由于物料在机构上，轴长“末端”绕法兰盘拍照位旋转同样的角度，携带物料运动到图中棕色位置（旋转位，与浅红位置平行），此时基准位减去棕色位置得到平移偏差，示教位为拍照位（第五点）T，T+平移偏差则可以将物料纠偏到基准位。综合纠偏位置=T+（基准位-运行位绕法兰盘得到的旋转位），基准位=M₉ * Image_{Mark基准点}+旋转半径（R），运行位=M₉ * Image_{Mark运行点}+旋转半径（R）。
（2）12点相对标定时，综合纠偏位置=T+（基准位-运行位绕原点得到的旋转位），基准位= M₁₂ * Image_{Mark基准点}，运行位= M₁₂ * Image_{Mark运行点}。
无论时单点抓取和单点纠偏，计算旋转偏差时，还需要考虑角度旋转一致性和物理坐标系与机构坐标的手性。VM中通常使用相对标定，即相对物理坐标系和像素坐标系的关系矩阵。

2.3 单相机平移抓取

单相机平移抓取，可以分两种情况进行分析，像素坐标系发生平移变换。
第一种情况：标定与生产时，相机发生平移。由于拍照位高度没有改变，相机虽然发生平移，但物理坐标系与像素坐标系的标定关系仍不变。因此当前相机的位置进行示教抓取即可。
第二种情况：生产时，相机需要发生固定的位移进行拍照来引导抓取。在第一个拍照位进行示教，可以将物料进行抓取。固定位移后在第二个拍照位时，对于视觉而言，无法察觉相机位移，可以直接计算平移偏差和旋转偏差。对于机构而言，拍照位发生固定位移，当示教位也平移固定位移，相当于第一个拍照位姿态，因此第二个拍照位抓取位置为T+固定位移+平移偏差+旋转偏差。

2.4 单相机旋转抓取

单相机旋转抓取，相比较标定时，抓取时相机发生旋转，像素坐标系发生旋转变换。
当相机发生旋转时（旋转轴），所拍摄的Mark点也会产生角度变化，因此需要将像素点绕图像旋转中心旋转，计算得到旋转前像素坐标系下该点的像素坐标。接下来则通过此像素坐标（基准点和运行点）和标定文件计算平移偏差和旋转偏差。

3 多相机定位

多相机定位，通常需要联立多个像素坐标系的矩阵关系，通常使用标定板标定、相机映射模块或映射标定模块。标定板标定模块，可以将像素坐标系与标定板坐标系建立矩阵关系。相机映射模块，需要获取两个相机拍同样物体的四组点，即要求相机需要排到同样的部分。映射标定模块，仅支持海康标定板，此标定板上带有二维码，则不需要相机拍到相同的部分（角点映射数目为0），直接输入两个相机拍到的标定板即可。相机映射模块或映射标定模块都支持静止映射和移动映射。

3.1 单点映射对位

针对对位贴合场景，上相机拍目标，下相机拍物料，最后将对象贴合到目标上。通常是下相机与机构进行12点标定得到标定文件M1，上相机与下相机进行联立得到映射标定文件M2。
生产时，上相机将目标Mark点，和贴合的直线（代表角度，角度无法直接进行标定转换）转换到下相机的像素坐标系中，最后将目标和对象都转换到物理坐标系中计算偏差。

3.2 各自基准对位

与单点映射对位场景一致，但当上下相机无法进行联立时，上下相机分别与机构进行12点标定。对下相机而言是纠偏动作，对上相机而言是放置动作。
其中，需要注意的是，纠偏是在盲抓物料，导致Mark点与法兰盘的关系发生改变，运行位与基准位有一个偏差；放置时，示教位是在纠偏基准姿态进行的动作，纠偏在运行位时，则需要重新示教进行放置。所以每次盲抓再进行放置时，放置的New示教位=Old示教位+纠偏偏差。

3.3 多相机抓取或纠偏

将多个相机的像素坐标系进行联立，统一到一个坐标系中，就是常规的单点抓取与单点纠偏。当上下相机无法进行联立时，则需要相机与机构分别进行标定，12点标定时，注意存在多个相对物理坐标系，通过拟合的旋转中心，可以计算相对物理坐标系的平移偏差量。